10329. Shell game

To pass the time, Bessie the cow and her friend Elsie like to play a version of a game they saw at the county fair.

To start, Bessie puts three inverted shells on a table and places a small round pebble under one of them (at least she hopes it is a pebble; she found it on the ground in one of the pastures). Bessie then proceeds to swap pairs of shells, while Elsie tries to guess the location of the pebble.

The standard version of the game the cows saw being played at the county fair allowed the player to see the initial location of the pebble, and then required guessing its final location after all the swaps were complete.

However, the cows like to play a version where Elsie does not know the initial location of the pebble and can guess the pebble location after every swap. Bessie, knowing the right answer, gives Elsie a score at the end equal to the number of correct guesses she made.

Given the swaps and the guesses, but not the initial pebble location, please determine the highest possible score Elsie could have earned.

Input. The first line contains an integer n (1 ≤ n ≤ 100) giving the number of swaps. Each of the next n lines describes a step of the game and contains three integers a, b and g, indicating that shells a and b were swapped by Bessie, and then Elsie guessed shell g after the swap was made. All three of these integers are either 1, 2 or 3, and a ≠ b.

Output. Print the maximum number of points Elsie could have earned.

Example. In this example, Elsie could have earned at most 2 points. If the pebble started under shell 1, then she is right exactly once (her final guess). If the pebble started under shell 2, then she is right twice (the first two guesses). If the pebble started under shell 3, then she doesn’t make any correct guesses.

Sample input	Sample output
3 1 2 1 3 2 1 1 3 1	2

SOLUTION

simulation

Algorithm analysis

The pebble may initially be under the first, second, or third shell. Let’s consider each of these three cases, and for each of them compute the number of points that Elsie will earn. The maximum of them will be the answer. The task reduces itself to a simulation of the game.

Example

Let’s simulate the game for three cases: when the pebble is first under the first, the second, and the third shells. The arrows indicate Elsie’s assumptions.

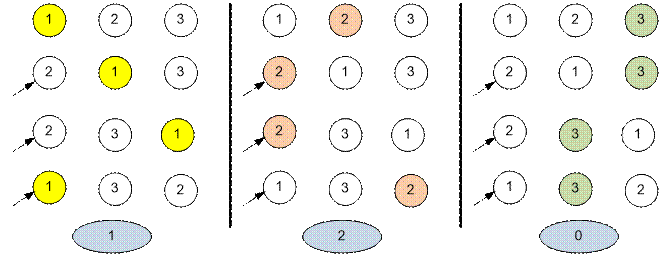
In the first case, Elsie will guess 1 time, in the second twice, and in the third 0 times. The maximum number of points that Elsie can earn is 2. This will be the case when the pebble is initially under shell number 2.

Algorithm realization

The game contains no more than 100 steps, let’s store them in arrays a, b and g.

int a[100], b[100], g[100];

Function num_correct returns the number of points earned by Elsie provided that the pebble is initially located under the shell number starting_shell. Initially current_shell = starting_shell.

int num_correct(int starting_shell)

{

The variable current_shell contains the number of the shell under which the pebble lies before each iteration.

int current_shell = starting_shell, correct = 0;

for (int i = 0; i < n; i++)

{

If the stone is at position a_i, then it should be moved to position b_i (and vice versa).

if (a[i] == current_shell) current_shell = b[i];

else if (b[i] == current_shell) current_shell = a[i];

If, after the exchange, the pebble is at position g_i, then Elsie guesses its position and earns one point.

if (current_shell == g[i]) correct++;

}

return correct;

}

The main part of the program. Read the input data.

scanf("%d", &n);

for (i = 0; i < n; i++)

scanf("%d %d %d", &a[i], &b[i], &g[i]);

Iterate over all the possible initial positions of the pebble: i = 1, 2, 3. For each of them, compute the number of Elsie’s points. In the variable best find the maximum among them.

int best = 0;

for (i = 1; i <= 3; i++)

best = max(best, num_correct(i));

Print the answer.

printf("%d\n", best);

Algorithm realization – simulation

Store the steps of the game in arrays a, b and g.

int a[100], b[100], g[100];

Read the input data.

scanf("%d", &n);

for (i = 0; i < n; i++)

scanf("%d %d %d", &a[i], &b[i], &g[i]);

In the variable best, compute the maximum score that Elsie can earn.

int best = 0;

Iterate through all the possible initial positions of the pebble: i = 1, 2, 3.

for (i = 1; i <= 3; i++)

{

The initial position of the game is encoded in the array m. Initially, the pebble lies under the shell i: set m[i] = 1 and set the remaining cells of the array m to zero.

int m[] = { 0, 0, 0, 0 };

m[i] = 1;

In the variable cnt compute the number of Elsie’s correct guesses.

cnt = 0;

In the array m simulate n steps of the game. Swap shells with numbers a[j] and b[j]. If m[g[j]] = 1, then Elsie’s conjecture is correct.

for (j = 0; j < n; j++)

{

swap(m[a[j]], m[b[j]]);

cnt += m[g[j]];

}

Find the maximum among all values of cnt.

if (cnt > best) best = cnt;

}

Print the answer.

printf("%d\n", best);

Python realization – simulation

Read the number of swaps n.

n = int(input())

Store the steps of the game in arrays a, b and g.

a = [0] * n

b = [0] * n

g = [0] * n

Read the data of the game.

for i in range(n):

a[i], b[i], g[i] = map(int, input().split())

In the variable best, compute the maximum score that Elsie can earn.

best = 0

Iterate through all the possible initial positions of the pebble: i = 1, 2, 3.

for i in range(1, 4):

The initial position of the game is encoded in the array m. Initially, the pebble lies under the shell i: set m[i] = 1 and set the remaining cells of the array m to zero.

m = [0, 0, 0, 0]

m[i] = 1

In the variable cnt compute the number of Elsie’s correct guesses.

cnt = 0

In the array m simulate n steps of the game. Swap shells with numbers a[j] and b[j]. If m[g[j]] = 1, then Elsie’s conjecture is correct.

for j in range(n):

m[a[j]], m[b[j]] = m[b[j]], m[a[j]]

cnt += m[g[j]]

Find the maximum among all values of cnt.

if cnt > best:

best = cnt

Print the answer.

print(best)